Коды, создаваемые с помощью одной лампочки
Теперь усложняем задачу: используем два разряда, или, в нашей "научной" терминологии — две лампочки. Сколько сигналов, или кодов, мы можем с их помощью обеспечить?
Это зависит от того, сколько комбинаций (битовых "слов") мы можем составить.
Замечание
В обычных словах играет роль последовательность элементов-букв. Когда мы говорим слово "да", мы используем две буквы — но сигнал-то один, т. к. обозначается одно конкретное слово. Эти две буквы сами по себе ничего не значат, кроме звуков. Только их сочетание имеет значение, дает тот самый код, который имеет соответствующий смысл. Если мы переставим элементы, то получим совсем другое слово — "ад", что характерно, не имеющее никакой связи с первым. Когда мы говорим "нет", мы используем три буквы, которые также сами по себе ничего не значат. Поэтому мы должны считать не буквы, а сочетания. Это напоминает позиционный принцип: если мы ставим один и тот же элемент (одну и ту же букву, цифру или, как в данном случае, одну и ту же лампочку) в разные позиции или их разные сочетания — мы получаем разные значения кодов.
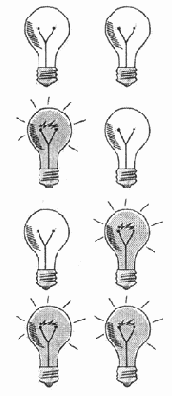
Итак, рассмотрим все возможные комбинации.
Желающие могут проверить: других вариантов не получится (рис. 5.2)! Следовательно, когда приходится использовать две лампочки (или два двоичных разряда), всегда получаются четыре кода.
До сих пор все кажется достаточно очевидным, но следующий шаг ("рассмотрим более сложный вариант из трех лампочек, или трех разрядов") всегда вызывает в аудиториях, далеких от математики, ошибочные мнения. Обычно чаще всего называют числа "6" или "9" (видимо, по аналогии: "три плюс три" или "три в квадрате"). И то и другое — ошибка.
Для преодоления ошибки составим таблицу, представив горящую лампочку "единицей", а негорящую — "нулем" (табл. 5.1).